Théorème des accroissements finis

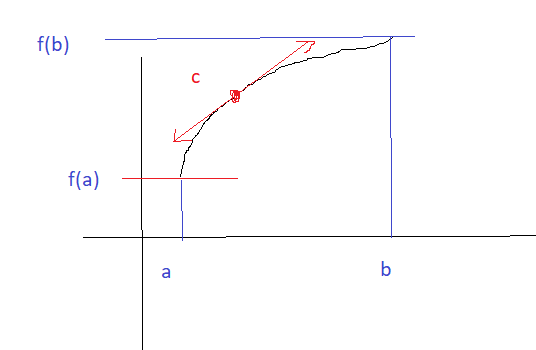
Soit $f:[a,b]$ $\to$ $\Bbb R$ une fonction continue sur $[a,b]$ et dérivable sur $]a,b[$. Alors $\exists c \in ]a,b[$ tel que $\frac{f(b)-f(a)}{b-a}=f'(c)$

Corollaire (inégalité des accroissements finis)

Soit $f:[a,b]\rightarrow\Bbb R$ continue sur $[a,b]$ et dérivable sur $]a,b[$.
Si $M=\sup|f'(x)|\lt +\infty$ alors $|f(b)-f(a)|\leq M|b-a|$
Exemple: $f(t)=arctan(t)$
$f$ est continue et dérivable sur $\Bbb R$ et $f'(t)=\frac{1}{1+t^2}$ et $f(0)=0$
En particulier $\sup |f'(t)|\leq 1$
D'aprés l'IAF:
$$|f(t)-f(0)|\leq |t-0|\sup|f'(t)|\leq |t|$$

Pour 2 variables

Théorème des accroissements finis pour 2 variables

Soit $f:U\to \Bbb R$ de la classe $C^1$ sur un ouvert $U\subset\Bbb R^2$
Si le segment $[a,b]\in U$, alors il existe $c\in]a,b[$ tel que:
$$f(b)-f(a)=\langle{grad(f(c))|b-a}\rangle $$

Corollaire du théorème des accroissments finis pour 2 variables

Soit $f:U\to\Bbb R$ de classe $C^1$ sur un ouvert $U$ convexe.
Si il existe $k$ tel que ${{||grad(f(c))\leq k||}},\quad \forall c\in U$
Alors:
$$\forall a,b\in U\quad {{|f(b)-f(a)|\leq k||b-a||}}$$

Fonction dont les dérivées partielles sont nulles

Soit $f:U\to \Bbb R$ de classe $C^1$ sur $U$ connexe.
Si ${{grad(f(x,y))=0}}, \quad \forall(x,y)\in U$ alors $f$ est une fonction constante sur $U$.